Home » Course Layouts » Free Course Layout Udemy
MAE 5790: Nonlinear Dynamics and Chaos (Spring 2014, Cornell University). Instructor: Professor Steven Strogatz. This course provides an introduction to nonlinear dynamics, with applications to physics, engineering, biology, and chemistry. It closely follows Prof. Strogatz's book, "Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering."
0
3
English
English [CC]
- Learn basic syntax that can apply to any language.
- Learn what is a programming language and the basic concepts for beginners.
- Understand what is Javascript in it's truest form.
- Know the basic syntax of Javascript.
- Know some hidden quirks in Javascript.
Description
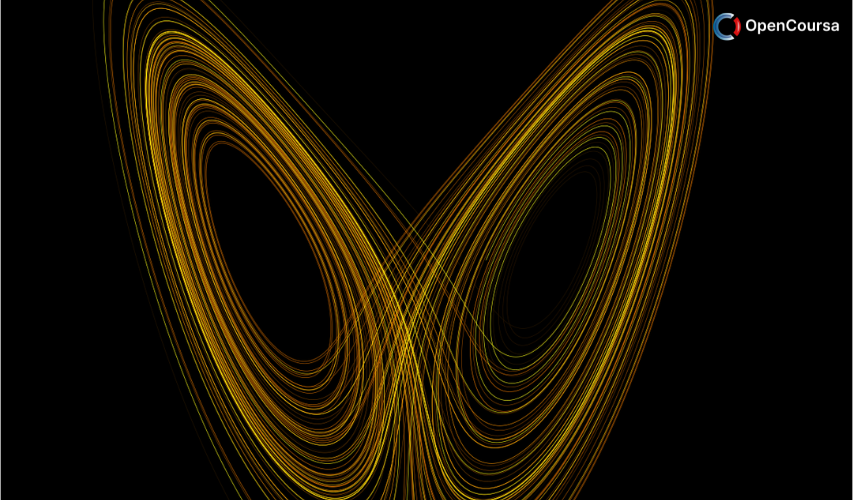
The mathematical treatment is friendly and informal, but still careful. Analytical methods, concrete examples, and geometric intuition are stressed. The theory is developed systematically, starting with first-order differential equations and their bifurcations, followed by phase plane analysis, limit cycles and their bifurcations, and culminating with the Lorenz equations, chaos, iterated maps, period doubling, renormalization, fractals, and strange attractors.
Course content
- Lecture 01 – Course Introduction and Overview Unlimited
- Lecture 02 – One Dimensional Systems Unlimited
- Lecture 03 – Overdamped Bead on a Rotating Hoop Unlimited
- Lecture 04 – Model of an Insect Outbreak Unlimited
- Lecture 05 – Two Dimensional Linear Systems Unlimited
- Lecture 06 – Two Dimensional Nonlinear Systems: Fixed Points Unlimited
- Lecture 07 – Conservative Systems Unlimited
- Lecture 08 – Index Theory and Introduction to Limit Cycles Unlimited
- Lecture 09 – Testing for Closed Orbits Unlimited
- Lecture 10 – Van der Pol Oscillator Unlimited
- Lecture 11 – Averaging Theory for Weakly Nonlinear Oscillators Unlimited
- Lecture 12 – Bifurcations in Two Dimensional Systems Unlimited
- Lecture 13 – Hopf Bifurcations in Aeroelastic Instabilities and Chemical Oscillators Unlimited
- Lecture 14 – Global Bifurcations of Cycles Unlimited
- Lecture 15 – Chaotic Waterwheel Unlimited
- Lecture 16 – Waterwheel Equations and Lorenz Equations Unlimited
- Lecture 17 – Chaos in the Lorenz Equations Unlimited
- Lecture 18 – Strange Attractor for the Lorenz Equations Unlimited
- Lecture 19 – One Dimensional Maps Unlimited
- Lecture 20 – Universal Aspects of Period Doubling Unlimited
- Lecture 21 – Feigenbaum’s Renormalization Analysis of Period Doubling Unlimited
- Lecture 22 – Renormalization: Function Space and a Hands-on Calculation Unlimited
- Lecture 23 – Fractals and the Geometry of Strange Attractors Unlimited
- Lecture 24 – Henon Map Unlimited
- Lecture 25 – Using Chaos to Send Secret Messages Unlimited
N.A
- 5 stars0
- 4 stars0
- 3 stars0
- 2 stars0
- 1 stars0
No Reviews found for this course.