Home » Course Layouts » Free Course Layout Udemy
Complex analysis is a basic tool with a great many practical applications to the solution of physical problems.
0
1
English
English [CC]
FREE
- Learn basic syntax that can apply to any language.
- Learn what is a programming language and the basic concepts for beginners.
- Understand what is Javascript in it's truest form.
- Know the basic syntax of Javascript.
- Know some hidden quirks in Javascript.
Description
It revolves around complex analytic functions—functions that have a complex derivative. Unlike calculus using real variables, the mere existence of a complex derivative has strong implications for the properties of the function. Applications reviewed in this class include harmonic functions, two dimensional fluid flow, easy methods for computing (seemingly) hard integrals, Laplace transforms, and Fourier transforms with applications to engineering and physics
Course content
- Course Introduction Unlimited
- Topic 1: Complex Algebra and the Complex Plane Unlimited
- Topic 1: Complex Algebra and the Complex Plane Unlimited
- Topic 2: Analytic Functions Unlimited
- Topic 2: Analytic Functions Unlimited
- Review of 18.02 Multivariable Calculus Unlimited
- Topic 3: Cauchy’s Theorem Unlimited
- Topic 4: Cauchy Integral Formula Unlimited
- Topic 5: Harmonic Functions Unlimited
- Topic 5: Harmonic Functions Unlimited
- Topic 6: Two Dimensional Hydrodynamics and Complex Potentials Unlimited
- Topic 6: Two Dimensional Hydrodynamics and Complex Potentials Unlimited
- Topic 7: Taylor and Laurent Series Unlimited
- Topic 8: Residue Theorem Unlimited
- Topic 9: Definite Integrals Using the Residue Theorem Unlimited
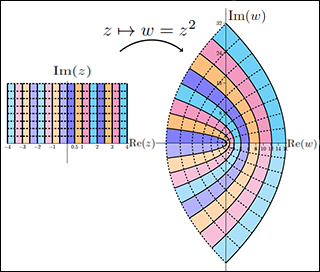
- Topic 10: Conformal Transformations Unlimited
- Topic 10: Conformal Transformations Unlimited
- Topic 10: Conformal Transformations Unlimited
- Topic 11: Argument Principle Unlimited
- Topic 12: Laplace Transform Unlimited
- Topic 13: Analytic Continuation and the Gamma Function Unlimited
Instructor
Massachusetts Institute of Technology
5
5
1
1916
1520
