Home » Course Layouts » Free Course Layout Udemy
Real Analysis. Instructor: Prof. S.H. Kulkarni, Department of Mathematics, IIT Madras. This course discusses the fundamental concepts in real analysis.
0
English
English [CC]
FREE
- Learn basic syntax that can apply to any language.
- Learn what is a programming language and the basic concepts for beginners.
- Understand what is Javascript in it's truest form.
- Know the basic syntax of Javascript.
- Know some hidden quirks in Javascript.
Description
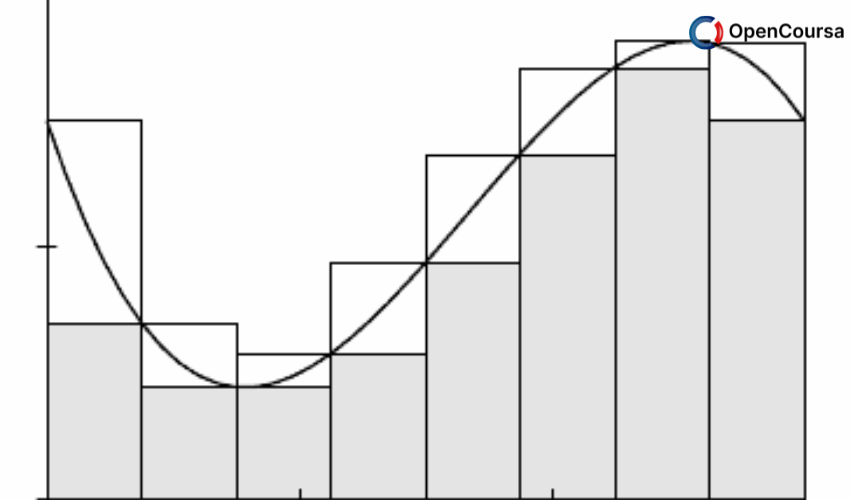
Real number system and its order completeness, sequences and series of real numbers. Metric spaces: basic concepts, continuous functions, completeness, contraction mapping theorem, connectedness, intermediate value theorem, compactness, Heine-Borel theorem. Differentiation, Taylor's theorem, Riemann integral, improper integrals, sequences and series of functions, uniform convergence, power series, Weierstrass approximation theorem, equicontinuity, Arzela-Ascoli theorem. (from nptel.ac.in)
Course content
-
- Lecture 01 – Introduction Unlimited
- Lecture 02 – Functions and Relations Unlimited
- Lecture 03 – Finite and Infinite Sets Unlimited
- Lecture 04 – Countable Sets Unlimited
- Lecture 05 – Uncountable Sets, Cardinal Numbers Unlimited
-
- Lecture 06 – Real Number System Unlimited
- Lecture 07 – Least Upper Bound (LUB) Axiom Unlimited
- Lecture 08 – Sequences of Real Numbers Unlimited
- Lecture 09 – Sequences of Real Numbers (cont.) Unlimited
- Lecture 10 – Sequences of Real Numbers (cont.) Unlimited
- Lecture 11 – Infinite Series of Real Numbers Unlimited
- Lecture 12 – Series of Nonnegative Real Numbers Unlimited
- Lecture 13 – Conditional Convergence Unlimited
- Lecture 14 – Metric Spaces: Definition and Examples Unlimited
- Lecture 15 – Metric Spaces: Examples and Elementary Concepts Unlimited
- Lecture 16 – Balls and Spheres Unlimited
- Lecture 17 – Open Sets Unlimited
- Lecture 18 – Closure Points, Limit Points and Isolated Points Unlimited
- Lecture 19 – Closed Sets Unlimited
- Lecture 23 – Limit and Continuity of a Function Defined on a Metric Space Unlimited
- Lecture 24 – Continuous Functions on a Metric Space Unlimited
- Lecture 25 – Uniform Continuity Unlimited
- Lecture 33 – Differentiation Unlimited
- Lecture 34 – Mean Value Theorems Unlimited
- Lecture 35 – Mean Value Theorems (cont.) Unlimited
- Lecture 36 – Taylor’s Theorem Unlimited
- Lecture 37 – Differentiation of Vector Valued Functions Unlimited
- Lecture 46 – Sequences and Series of Functions Unlimited
- Lecture 47 – Uniform Convergence Unlimited
- Lecture 48 – Uniform Convergence and Integration Unlimited
- Lecture 49 – Uniform Convergence and Differentiation Unlimited
- Lecture 50 – Construction of Everywhere Continuous, Nowhere Differentiable Function Unlimited
- Lecture 51 – Approximation of a Continuous Function by Polynomials: Weierstrass Theorem Unlimited
- Lecture 52 – Equicontinuous Family of Functions: Arzela-Ascoli Theorem Unlimited
Instructor
OpenCoursa
Accessible Education for Everyone
5
5
6
24186
4637
We are an educational and skills marketplace to accommodate the needs of skills enhancement and free equal education across the globe to the millions. We are bringing courses and trainings every single day for our users. We welcome everyone woth all ages, all background to learn. There is so much available to learn and deliver to the people.
