0
(
ratings
)
students
Created by:
Last updated:
Duration:
This course includes:
Unlimited Duration
Badge on Completion
Certificate of completion
Unlimited Duration
Description
Basics of Finite Element Analysis. Instructor: Prof. Nachiketa Tiwari, Department of Mechanical Engineering, IIT Kanpur.
This course is intended for all those who want to learn Finite Element Analysis from an application standpoint. Currently, many users of FEA have limited understanding of theoretical foundation of this powerful method. The consequence is that quite often they use commercial codes inaccurately, and do not realize that their results may be flawed. The course is intended to address this limitation by making the student aware of the underlying mathematics in easy to understand format. The course is open to all engineering students who have at the minimum successfully completed two years of their B. Tech (or equivalent) degrees. The course is also open to all professionals in industry who wish to learn fundamentals of FEA in a semi-formal but structured setting, and plan to use this knowledge in their workplace. (from nptel.ac.in)
Course Curriculum
- Lecture 01 – Introduction to Finite Element Analysis (FEA) Unlimited
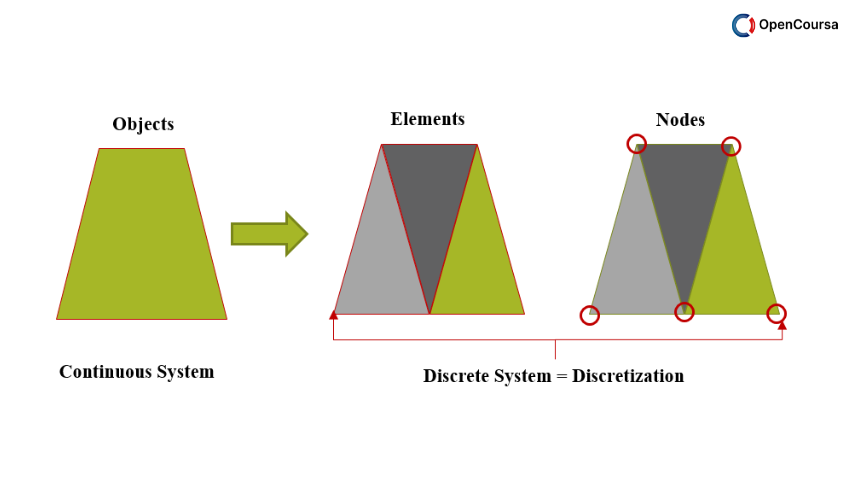
- Lecture 02 – Philosophy of FEA, Nodes, Elements and Shape Functions Unlimited
- Lecture 03 – Nodes, Elements and Shape Functions Unlimited
- Lecture 04 – Polynomials as Shape Functions, Weighted Residuals, Elements and Assembly Level Equations Unlimited
- Lecture 05 – Types of Errors in FEA, Overall FEA Process and Convergence Unlimited
- Lecture 06 – Strengths of Finite Element Method, Continuity Conditions at Interfaces Unlimited
- Lecture 07 – Key Concepts and Terminologies Unlimited
- Lecture 08 – Weighted Integral Statements Unlimited
- Lecture 09 – Integration by Parts – Review Unlimited
- Lecture 10 – Gradient and Divergence Theorems Unlimited
- Lecture 11 – Gradient and Divergence Theorems (cont.) Unlimited
- Lecture 12 – Functionals Unlimited
- Lecture 13 – Variational Operator Unlimited
- Lecture 14 – Weighted Integral and Weak Formulation Unlimited
- Lecture 15 – Weak Formulation Unlimited
- Lecture 16 – Weak Formulation and Weighted Integral: Principle of Minimum Potential Energy Unlimited
- Lecture 17 – Variational Methods: Rayleigh Ritz Method Unlimited
- Lecture 18 – Rayleigh Ritz Method Unlimited
- Lecture 19 – Method of Weighted Residuals Unlimited
- Lecture 20 – Different Types of Weighted Residual Methods Unlimited
- Lecture 21 – Different Types of Weighted Residual Methods (cont.) Unlimited
- Lecture 22 – FEA Formulation for Second Order Boundary Value Problem Unlimited
- Lecture 23 – FEA Formulation for Second Order Boundary Value Problem (cont.) Unlimited
- Lecture 24 – Element Level Equations Unlimited
- Lecture 25 – Second Order Boundary Value Problem Unlimited
- Lecture 26 – Assembly of Element Equations Unlimited
- Lecture 27 – Assembly of Element Equations, Implementation of Boundary Conditions Unlimited
- Lecture 28 – Assembly Process and Connectivity Matrix Unlimited
- Lecture 29 – Radially Symmetric Problems Unlimited
- Lecture 30 – One Dimensional Heat Transfer Unlimited
- Lecture 31 – 1D-Heat Conduction with Convective Effects; Examples Unlimited
- Lecture 32 – Euler-Bernoulli Beam Unlimited
- Lecture 33 – Interpolation Functions for Euler-Bernoulli Beam Unlimited
- Lecture 34 – Finite Element Equations for Euler-Bernoulli Beam Unlimited
- Lecture 35 – Assembly Equations for Euler-Bernoulli Beam Unlimited
- Lecture 36 – Boundary Conditions for Euler-Bernoulli Beam Unlimited
- Lecture 37 – Shear Deformable Beams Unlimited
- Lecture 38 – Finite Element Formulation for Shear Deformable Beams Unlimited
- Lecture 39 – Finite Element Formulation for Shear Deformable Beams (cont.) Unlimited
- Lecture 40 – Equal Interpolation but Reduced Integration Element Unlimited
- Lecture 41 – Eigenvalue Problems Unlimited
- Lecture 42 – Eigenvalue Problems: Examples Unlimited
- Lecture 43 – Introduction to Time Dependent Problems Unlimited
- Lecture 44 – Spatial Approximation Unlimited
- Lecture 45 – Temporal Approximation for Parabolic Problems Unlimited
- Lecture 46 – Temporal Approximation for Parabolic Problems (cont.) Unlimited
- Lecture 47 – Temporal Approximation for Hyperbolic Problems Unlimited
- Lecture 48 – Explicit and Implicit Methods, Diagonalization of Mass Matrix Unlimited
About the instructor
Instructor Rating
Reviews
Courses
Students
