Home » Course Layouts » Free Course Layout Udemy
Introduction to Finite Volume Methods I. Instructor: Prof. Ashoke De, Department of Aerospace Engineering, IIT Kanpur.
0
English
English [CC]
- Learn basic syntax that can apply to any language.
- Learn what is a programming language and the basic concepts for beginners.
- Understand what is Javascript in it's truest form.
- Know the basic syntax of Javascript.
- Know some hidden quirks in Javascript.
Description
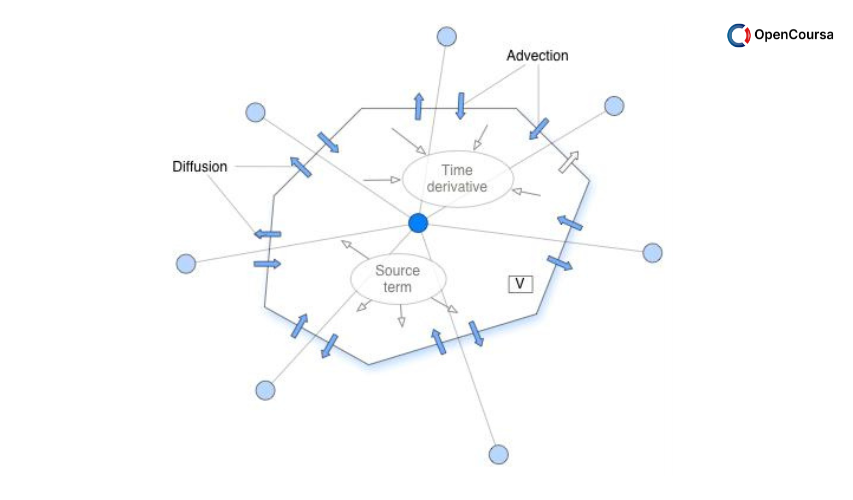
The Finite Volume Method (FVM) is one of the widely used numerical techniques in the scientific community and in industry as well. In this approach, the partial differential equations that represent the conservation laws to simulate uid flow, heat transfer, and other related physical phenomena, are transformed over differential volumes into discrete algebraic equations over nite volumes (or elements or cells). Thereafter, the system of algebraic equations is solved to compute the values of the dependent variable for each of the elements to represent the physical processes. (from nptel.ac.in)
Course content
-
- Lecture 01 – Introduction Unlimited
- Lecture 02 – Governing Equations and Discretization Unlimited
- Lecture 03 – Boundary Conditions and Classification of PDEs Unlimited
- Lecture 04 – Mathematical Description of Fluid Flow Unlimited
- Lecture 05 – Mathematical Description of Fluid Flow (cont.) Unlimited
-
- Lecture 06 – Discretization Process I Unlimited
- Lecture 07 – Discretization Process II Unlimited
- Lecture 08 – Discretization Process III Unlimited
- Lecture 09 – Taylor Series Unlimited
- Lecture 10 – Taylor Series (cont.) Unlimited
- Lecture 11 – Derivatives and Errors Unlimited
- Lecture 12 – Derivatives and Errors (cont.) Unlimited
- Lecture 13 – Grid Transformation Unlimited
- Lecture 14 – Finite Volume Formulation Unlimited
- Lecture 15 – Finite Volume Formulation (cont.) Unlimited
- Lecture 21 – Properties of Unstructured Mesh Unlimited
- Lecture 22 – Properties of Unstructured Mesh (cont.) Unlimited
- Lecture 23 – Finite Volume Discretization of Diffusion Equation I Unlimited
- Lecture 24 – Finite Volume Discretization of Diffusion Equation II Unlimited
- Lecture 25 – Finite Volume Discretization of Diffusion Equation III Unlimited
- Lecture 31 – Discretization of Diffusion Equation for Non-Orthogonal Systems II Unlimited
- Lecture 32 – Discretization of Diffusion Equation for Non-Orthogonal Systems III Unlimited
- Lecture 33 – Gradient Calculation for Diffusion Equation I Unlimited
- Lecture 34 – Gradient Calculation for Diffusion Equation II Unlimited
- Lecture 35 – Gradient Calculation for Diffusion Equation III Unlimited
N.A
- 5 stars0
- 4 stars0
- 3 stars0
- 2 stars0
- 1 stars0
No Reviews found for this course.